Class Conditional Independence - Naive Bayes Classifier
Table of contents
A set of straightforward probabilistic classifiers known as the Naive Bayes classifier are based on Bayes' theorem and assume high feature independence. The probability of an event occurring in relation to the probability of another event that has already occurred is determined by Bayes' Theorem. The following equation describes mathematically Bayes' theorem:
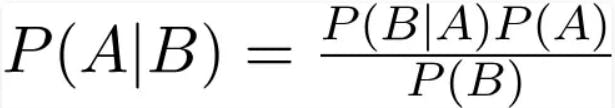
Types of Naive Bayes Classifiers
Multinomial Naive Bayes
The frequencies at which particular events are generated by a multinomial distribution are represented by feature vectors. Take, for instance, the count of how frequently each word appears in the document. The event model that is typically used for document classification is Multinomial Naive Bayes. It considers a feature vector where a term represents the number of times it appears or very often. It is mostly used in "Natural Language Processing".
Bernoulli Naive Bayes
This is like the multinomial naive bayes but the predictors are boolean variables either 1s or 0s. It accepts features that are a success(1s) or failure(0s), yes(1s) or no(0s), true or false, and so on.
Categorical Naive Bayes
This is like the bernoulli naive bayes model. It takes discrete, non-negative categories. Here, each feature may have at least two categories and each feature may have a different total number of categories. A categorical distribution is used to select the categories for each feature.
Gaussian Naive Bayes
It takes numeric features, i.e., assumes the likelihood of features in the P(x|y) terms is Gaussian. Each label's data is assumed to come from a straightforward Gaussian distribution in this classifier. A Gaussian distribution with no covariance between dimensions is used to describe the data. To define such a distribution, all that is required to fit this model is the mean and standard deviation of the points in each label.
Complement Naive Bayes
It takes non-negative categorical features and numeric features; similar to multinomial naive bayes but better for imbalanced datasets where the distribution of targets is not uniform.
Use Cases of Naive Bayes Model
Sentiment analysis, spam filtering, recommendation systems, and other similar applications typically employ Naive Bayes algorithms. Because of its higher success rates than those of other machine learning algorithms, it is primarily used for text classification tasks. They can be used for real-time prediction because they are quick and simple to implement. However, their biggest drawback is that predictors must be independent. Predictors that depend on most real-world scenarios hinder the classifier's performance.
Let's take an example to implement the Naive Bayes Model
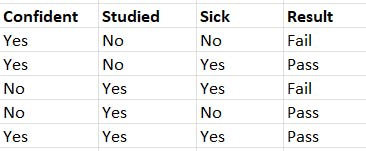
import pandas as pd
data = pd.DataFrame({'Confident' : ['Yes','Yes','No','No','Yes'], 'Studied' : ['No','No','Yes','Yes','Yes'],'Sick' : ['No','Yes','Yes','No','Yes'], 'Result' : ['Fail','Pass','Fail','Pass','Pass']})
from sklearn.preprocessing import LabelEncoder
col = list(data.columns)
model = LabelEncoder()
data[col] = data[col].apply(model.fit_transform)
As you look at the data clearly, we have the data as binary features. So, we prefer using the Bernoulli Naive Bayes model.
x = data.iloc[:,0:3]
y = data.Result
from sklearn.naive_bayes import BernoulliNB
BnB = BernoulliNB()
BnB.fit(x,y)
y_pred = BnB.predict(x)
We shall test our model with Confident - Yes, Studied - Yes, and Sick - No.
BnB.predict([[1,1,0]])
The predicted result will be Pass.